Pdf and cdf of a continuous random variable
Posted: Sun Aug 21, 2016 3:25 pm
A continuous random variable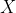 
has a pdf of the form
$f(x)=\begin{cases}ce^{-2x}&x>1\\0&x\leq1,\end{cases}$where
is a constant. Find the value of and the cdf of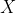 
.
If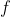
is a pdf, then we must have \,dx=1)
, so we simply need to solve for the value of . That is,
$\int_{-\infty}^\infty f(x)\,dx$ $=\int_{-\infty}^\infty ce^{-2x}\,dx$ $=\int_1^\infty ce^{-2x}\,dx$ $=\left.-\frac{c}{2}e^{-2x}\right|_{x=1}^\infty$ $=\frac{c}{2}e^{-2}=1\Rightarrow c=2e^2.$
Then the cdf of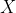 is ={\rm P}(X\leq x)=\int_{-\infty}^x f(v)\,dv=\begin{cases}0&{\rm if\ }x<1\\1-e^{2-2x}&{\rm if\ } x\geq1.\end{cases})
$f(x)=\begin{cases}ce^{-2x}&x>1\\0&x\leq1,\end{cases}$where
If
$\int_{-\infty}^\infty f(x)\,dx$ $=\int_{-\infty}^\infty ce^{-2x}\,dx$ $=\int_1^\infty ce^{-2x}\,dx$ $=\left.-\frac{c}{2}e^{-2x}\right|_{x=1}^\infty$ $=\frac{c}{2}e^{-2}=1\Rightarrow c=2e^2.$
Then the cdf of